Kepler’s Laws of Planetary Motion

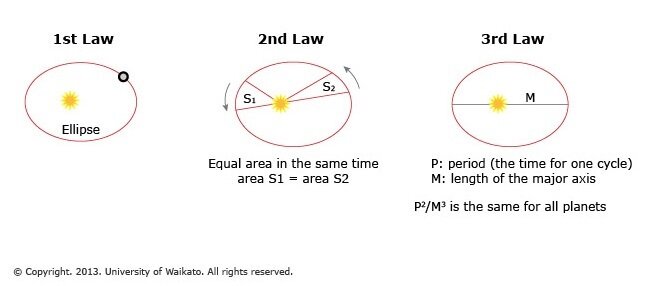
Kepler’s laws of planetary motion are composed of three laws that describe the motion and orbit of planets around the sun. Kepler’s first law of planetary motion states that the planets have an elliptical orbit around the sun with the sun located at one of the foci. What does this mean? Well, contrary to popular belief, the earth does not have a circular orbit around the sun. Although it is close to being a circular orbit, the earth’s orbit around the sun would be characterized as being more of an oval shape. This means that we don’t apply circular properties to the orbit of the earth, but rather properties of an ellipse which is a geometric shape. In a circle, you know that there is a center in which it is a measure of the radius of the circle away from the curvature of the circle. Similarly, in an ellipse, there are two foci in which have their own special connection to the points lying on the curvature of the ellipse. The sun lies at one of the foci in the elliptical orbit. Kepler’s second law of planetary motion states that there is a radius vector that joins the planet to the sun, and this radius vector forms an equal area in an equal interval of time. So, what does this mean? Well, let's talk about angular momentum for a second. Orbital Angular Momentum follows the equation L=pvsin(theta) where p is the linear momentum of the object, r is the radius between the object and a fixed point, and theta is the angle between the linear momentum vector and the radius vector. If we consider the Earth to be the object and the sun to be the fixed point, we can apply the principles of angular momentum to describe the orbit of the Earth around the sun as we can assume that angular momentum is conserved throughout the orbit. Thus, according to the concept of Conservation of Angular Momentum and the equation, L=psin(theta), we know that at a point where the earth has a lesser radius from the sun in its elliptical orbit, the tangential velocity must be greater, and when the earth has a greater radius away from the sun in its elliptical orbit, the earth must have lesser tangential velocity. This means that in an equal amount of time that has passed at these particular points, the area formed by the triangle between the former position of the earth, the current position of the earth, and the sun in both cases must be equal to each other. This is because the greater velocity means it travels farther, although it is closer to the sun, while a lesser velocity means it doesn’t travel as far, although it is farther from the sun. Through this examination, we can see how Kepler’s second law works. Kepler’s third law, in equation form, is ((T^2)/(R^3))=(4pi^2)/(GM). In this equation, T represents the orbital period of the planet around the sun, R represents the semi-major axis from the planet to the sun(think radius of a circle but in the form of the longways part of the ellipse), G represents the gravitational constant, and M represents the mass in which the planet is orbiting. This law connects several different concepts involved in planetary motion as shown above. This equation is cool because it also can be used to calculate the orbits of satellites around the earth. Well, now you can explain to your friend how the earth moves around the sun.

Kepler’s laws of planetary motion

Picture Source: University Waikato