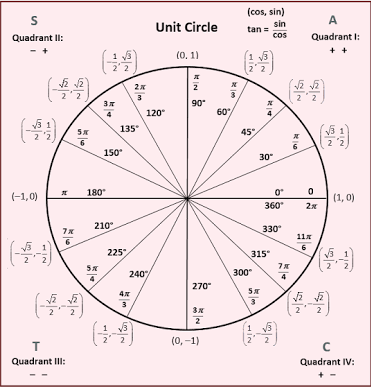
The Unit Circle

The unit circle is a useful tool that helps find the sines, cosines, and tangents of angles quickly! This graphed circle with a radius of 1 unit and that is centered on the origin (0, 0) can give the sines, cosines, and tangents of multiples of 30 degree angles, 45 degree angles, 60 degree angles, and 90 degree angles. In radians, π is equal to 180 degrees, or half a circle, and 2π is equal to 360 degrees, or a full circle. Using this, the unit circle can also lead to the sines, cosines, and tangents of the equivalent radian values of π/6, π/4, π/3 and π/2.

On a graph, these angles eventually converge with the unit circle and the point where they intersect gives coordinates which can help solve trigonometric functions. It’s almost like the clock for mathematicians, but instead of telling time it gives answers! As you go farther along the x-axis from the center of the graph, the x values for the coordinates of multiples of 30 degree angles, 45 degree angles, and 60 degree angles will increase in value from 1/2, to √2/ 2, and to √3/2. Likewise, the pattern for the y values of the y-axis will also be the elevation from 1/2, to √2/ 2, and to √3/2. Knowing this pattern would not only allow you to be able to draw this circle any time you want, but with more practice would also allow you to imagine the values without needing a paper or pen! For example, an easy way to find the y value and x value of the coordinate for 60 degrees would be to remember that 60 degrees is the “highest” angle in the pattern so its y value would be the last y value in the pattern,√3/2 . It also the angle that is closest to the the origin on the x-axis, so its x value would then be the first value in the pattern, 1/2.

The sine for any of these angles, including the angles that are multiples of 90 degrees, will always be equal to the y value of the corresponding coordinate. Similarly, the cosine for any of these angles will always be equal to the x value of each coordinate. Finally, by using the equation tan (θ) = sin(θ)/cos(θ) which can be rewritten as the equation , the tangent can also tan (θ) = x /y then be easily found by plugging in the y values and x values that are given. With practice, the unit circle will allow you to solve most trigonometry problems without needing to pick up a calculator!

Picture Source: socratic.org